オイラー法と同様に常微分方程式の基本形
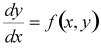
(1)
において座標点
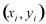
を考え、
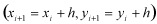
における
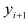
を求めたいとします。hは微小な値とします。そこでテイラー展開
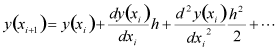
(2)
を用いますが、オイラー法ではテイラー展開を1次までしかとりませんでした。修正オイラー法では2次の項まで考えます。そうすると
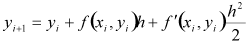
(3)
という式が得られますが、この式には関数fを微分したものが含まれいるため計算が面倒です。そこで、
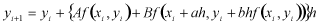
(4)
と関数fを微分したものを含まない形で表せるとします。ここで、
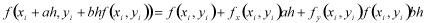
(5)
と1次までテイラー展開して、式(5)を式(4)へ代入して、
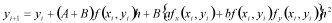
(6)
という式が得られます。ここで、
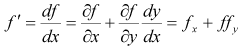
(7)
であるから、式(3)と式(6)を比べて、A = B = 1/2、a = b = 1 とすると両者は等しくなる事がわかります。よって、次の式が得られます。
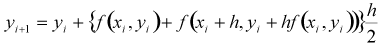
(8)
修正オイラー法ではこの式を用いて数値計算を行います。また、プログラムのソースコードを書く際に、考えやすいように次のような形に式を書いておくと便利です。
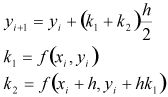
(9)
ここでは単振動の問題を修正オイラー法を使って解いてみます。質量の値とばね定数の値を1とすると運動方程式は
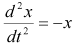
(10)
となりますが次のように変形します。
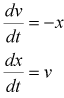
(11)
vは速度です。常微分方程式が2つ出てきましたが難しいことはありません。それぞれに修正オイラー法を適用して解いていきます。
#include <stdio.h>
double f1(double x,double v);
double f2(double x,double v);
int main()
{
double t,dt,x,v,tmax;
double k0[2],k1[2];
dt=0.01; //刻み幅設定
x=1.0; //位置初期値
v=0.0; //速度初期値
tmax=100; //繰り返し最大回数
FILE *output;
output=fopen("output.data","w");
fprintf(output,"%f %f\n",x,v);
for(t=0;t<tmax;t+=dt) {
k0[0]=f1(x,v);
k0[1]=f2(x,v);
k1[0]=f1(x+dt*k0[0],v+dt*k0[1]);
k1[1]=f2(x+dt*k0[0],v+dt*k0[1]);
x=x+dt*(k0[0]+k1[0])/2.0;
v=v+dt*(k0[1]+k1[1])/2.0;
fprintf(output,"%f %f\n",x,v);
}
fclose(output);
return 0;
}
double f1(double x,double v)
{
return v;
}
double f2(double x,double v)
{
return (-x);
}
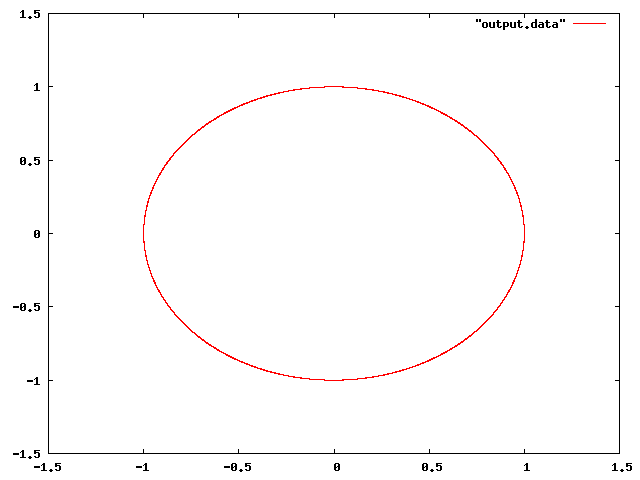
下の画像は数値計算の結果をGNUPLOTで表示したものです。横軸が位置xを表し、縦軸が速度vを表しています。単振動において、外部からの力や摩擦や抵抗がなければ、位置と速度の最大値と最小値は変わらないから、一定の円を描くはずです。修正オイラー法で解いた結果はまさにそうなっています。しかし、プログラム内の繰り返し最大回数を大幅に増やすと、一定の円から軌道がずれてくる事がわかります。
オイラー法よりは誤差の影響がずいぶんと小さくなった修正オイラー法ですが、この方法よりももっと精度に優れたルンゲクッタ法というものがあります。
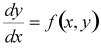 (1)
(1)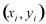 を考え、
を考え、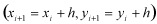 における
における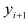 を求めたいとします。hは微小な値とします。そこでテイラー展開
を求めたいとします。hは微小な値とします。そこでテイラー展開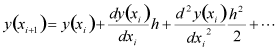 (2)
(2)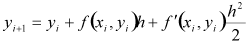 (3)
(3)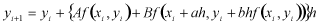 (4)
(4)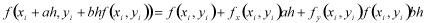 (5)
(5)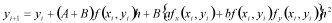 (6)
(6)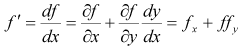 (7)
(7)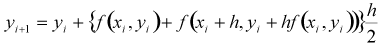 (8)
(8)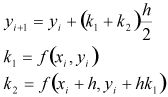 (9)
(9)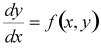 (1)
(1)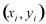 を考え、
を考え、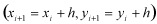 における
における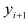 を求めたいとします。hは微小な値とします。そこでテイラー展開
を求めたいとします。hは微小な値とします。そこでテイラー展開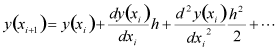 (2)
(2)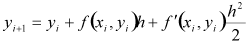 (3)
(3)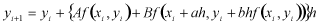 (4)
(4)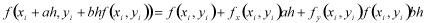 (5)
(5)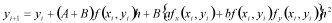 (6)
(6)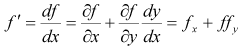 (7)
(7)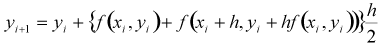 (8)
(8)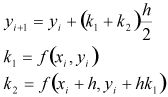 (9)
(9)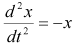 (10)
(10)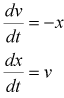 (11)
(11)