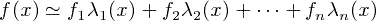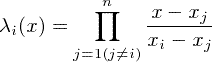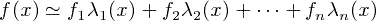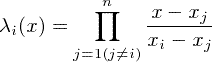ラグランジュの補間法

ラグランジュの補間法は、ある区間において存在する離散的なデータを、多項式で近似する時に使われます。ラグランジュの補間法の公式は、以下のように書かれます。

以下は、ラグランジュの補間法を用いて、データから近似的多項式を求め、その結果求まった近似的曲線データをファイルに出力するプログラムソースコード例です。 プログラムには、データが書き込まれたファイル（ input.dat ）が必要となります。今回は、適当に値を決めた input.dat を用います。

#include <stdio.h>
#include <stdlib.h>
 
#define NMAX 100    /* 配列最大要素数 */
 
double lambda(int, int, double, double *);    /* λ(x)を求める関数 */
 
int main(void)
{
    int i;
    int n;    /* データの個数 */
 
    double x;    /* x */
    double f;    /* f(x) */
 
    double data_x[NMAX];    /* データのx */
    double data_f[NMAX];    /* データのf(x) */
 
    FILE *input;
    FILE *output;
 
    /* ファイルオープン処理 */
    input = fopen("input.dat", "r");
    output = fopen("output.dat", "w");
 
    /* 配列初期化 */
    for(i = 0 ; i < NMAX ; i++)
    {
        data_x[i] = 0.0;
        data_f[i] = 0.0;
    }
 
    i = 0;    /* 一度使ったiを0に初期化 */
    
    /* ファイルからデータを取得 */
    while(fscanf(input, "%lf%lf", &data_x[i], &data_f[i]) != EOF)
    {
        i++;    /* 次のデータを、次の配列要素に入れるためにインクルメント */
        n = i;    /* データの個数を代入 */
    }
 
    /* ラグランジュの補間公式に基づく処理 */
    for(x = data_x[0] ; x < data_x[n-1] ; x += 0.1)
    {
        f = 0.0;
        for(i = 0 ; i < n ; i++)
        {
            f += data_f[i] * lambda(i, n, x, data_x);
        }
 
        fprintf(output, "%f %f\n", x, f);    /* ファイルへ書き込み */
    }
 
    fclose(input);    /* ファイルを閉じる */
    fclose(output);    /* ファイルを閉じる */
 
    return 0;
}
 
/* λ(x)を求める関数 */
double lambda(int i, int n, double x, double data_x[])
{
    int j;
    double lam = 1.0;
 
    for(j = 0 ; j < n ; j++)
    {
        if(i != j)
        {
            lam *= (x - data_x[j])/(data_x[i] - data_x[j]);
        }
    }
 
    return lam;
}
 

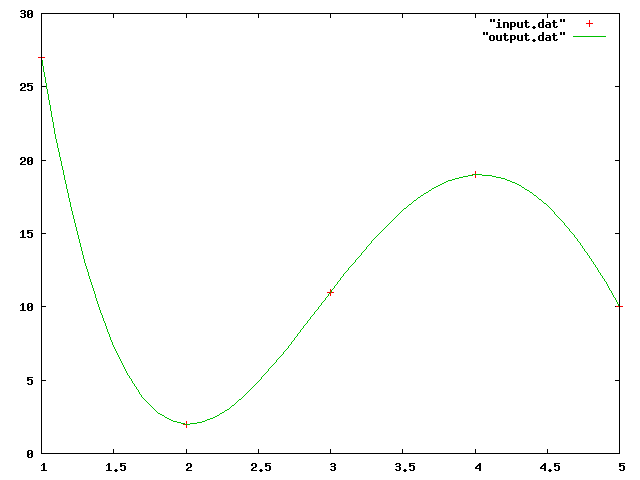
プログラムが正しく実行されると、output.dat ファイルができます。そのファイル内に近似的に求められた曲線データが書かれていますので、それを gnuplot で出力すると、以下の図のようになります。赤い５つの点は、input.dat をプロットしたものです。緑色の曲線は、ラグランジュの補間法を用いて、近似的に求めた曲線です。その曲線を見ると、データ間が上手く補間されているのがわかります。