n個の未知数
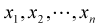
が含まれるn個の連立1次方程式
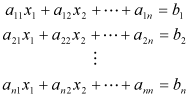
(1.1)
の解を求めるための1つの方法にヤコビ法と呼ばれる反復法があります。(1.1)は
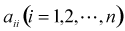
(1.2)
が0でなければ次のように変形できます。
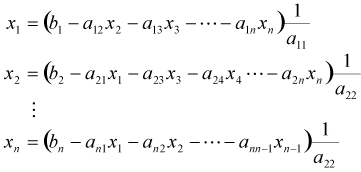
(1.3)
各式の左辺にはn個の未知数、すなわち求めたい解があります。よって右辺が求まっていれば左辺にある未知数が求まります。しかし、右辺にも未知数があります。
そこで、ヤコビ法ではまず全ての未知数の値を適当に決めます。そして、(1.3)の右辺に代入します。そうすると未知数に計算された値が入ります。もし、適当に決めた未知数の値が、真の解であったら新たな解と一致するはずですが、普通そうは上手くいきません。しかし、新たな解は真の解に近づきます。実際は真の解に近づかないこともあります。
得られた新たな解を上記の式の右辺に代入するとまた新たな解が得られます。これらを繰り返して得られた解と一つ前に求めた解が、ある精度内で一致したらそこで終了し解とみなします。
プログラムでは上記の通り計算を進めても、新たな解が真の解に近づかない可能性もありますので、無限ループになってしまわないように繰り返し行う計算回数の上限値を決めておく必要があります。
#include <stdio.h>
#include <math.h>
#define n 3 //未知数の個数
#define max 100 //繰り返し最大回数
#define eps 1.0e-5 //最小誤差許容範囲
int main()
{
int i,j,k;
double err;
/*配列a,bには係数の値等を。配列xoldには適当に決めた解の値を入れておく*/
double a[n][n]={{3.0,-6.0,9.0},{2.0,5.0,-8.0},{1.0,-4.0,7.0}},
b[n]={6.0,8.0,2.0},xold[n]={1.0,1.0,1.0},xnew[n];
for(k=0;k<max;k++) {
err=0.0; //誤差のリセット
for(i=0;i<n;i++) {
xnew[i]=b[i];
for(j=0;j<n;j++) {
if(j!=i) {
xnew[i]-=a[i][j]*xold[j];
}
}
xnew[i]=xnew[i]/a[i][i];
}
/*各解の誤差を足し、古い解は捨て配列xoldに新しい解を入れる*/
for(i=0;i<n;i++) {
err+=fabs(xold[i]-xnew[i]);
xold[i]=xnew[i];
}
/*足しあわされた誤差が許容範囲内だったら
計算終了とし解が求まったとする*/
if(err<eps) break;
}
/*求まった解を出力する*/
for(i=0;i<n;i++) {
printf("%8.4f\n",xnew[i]);
}
/*繰り返し回数が最大回数の値だったら
正確な解が求まっていない可能性大なので注意*/
printf("繰り返し回数は %d\n",k+1);
return 0;
}
解が求まると以下のように表示されます。繰り返し回数が最大回数と一致した場合、正確な解が求まっていない可能性がありますので注意が必要です。
3.0000
2.0000
1.0000
繰り返し回数は 82
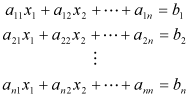 (1.1)
(1.1)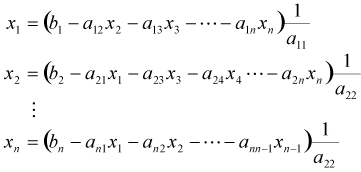 (1.3)
(1.3)