未知数 n 個を含む、n 個の方程式からなる連立1次方程式
 (1.2)
(1.2)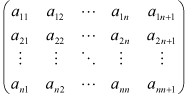 (1.3)
(1.3)ここらはこの行列を三角行列に変えていく方法を説明します。まず第1行を
 (1.4)
(1.4)しかし、この計算方法で、もし
 (1.2)
(1.2)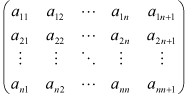 (1.3)
(1.3) (1.4)
(1.4)#include <stdio.h>
#include <math.h>
#define N 4 //未知数の数
/*計算結果を表示する際に、三角行列になったか
確認したいときは1を、解のみ表示した場合は0にしておく*/
#define CHECK 1
void gauss(double a[N][N+1])
{
int i,j,k,l,pivot;
double x[N];
double p,q,m,b[1][N+1];
for(i=0;i<N;i++) {
m=0;
pivot=i;
for(l=i;l<N;l++) {
/*i列の中で一番値が大きい行を選ぶ*/
if(fabs(a[l][i])>m) {
m=fabs(a[l][i]);
pivot=l;
}
}
/*pivotがiと違えば、行の入れ替え*/
if(pivot!=i) {
for(j=0;j<N+1;j++) {
b[0][j]=a[i][j];
a[i][j]=a[pivot][j];
a[pivot][j]=b[0][j];
}
}
}
for(k=0;k<N;k++) {
p=a[k][k]; //対角要素を保存
/*対角要素は1になることがわかっているので直接代入*/
a[k][k]=1;
for(j=k+1;j<N+1;j++) {
a[k][j]/=p;
}
for(i=k+1;i<N;i++) {
q=a[i][k];
for(j=k+1;j<N+1;j++) {
a[i][j]-=q*a[k][j];
}
/*0となることがわかっているので直接代入*/
a[i][k]=0;
}
}
/*解の計算*/
for(i=N-1;i>=0;i--) {
x[i]=a[i][N];
for(j=N-1;j>i;j--) {
x[i]-=a[i][j]*x[j];
}
}
/*行列が最後どうなったか見たいときに実行*/
#if CHECK==1
for(i=0;i<N;i++) {
for(j=0;j<N+1;j++) {
printf("%10.3f",a[i][j]);
}
printf("\n");
}
#endif
printf("解は\n");
for(i=0;i<N;i++) {
printf("%f\n",x[i]);
}
}
int main(void)
{
/*テストデータ用(プログラムが正常に動いているかの確認用)
3つの解1,2,3がでる。未知数の個数Nは3にする必要あり*/
/*double a[N][N+1]={{4.0,1.0,1.0,9.0},
{1.0,3.0,1.0,10.0},
{2.0,1.0,5.0,19.0}
};*/
double a[N][N+1]={{1.0,1.0,-3.0,-4.0,-1.0},
{2.0,1.0,5.0,1.0,5.0},
{3.0,6.0,-2.0,1.0,8.0},
{2.0,2.0,2.0,-3.0,2.0}};
/*解きたい連立方程式から行列をつくり配列a[N][N+1]に入れ、
関数gaussに渡す*/
gauss(a);
return 0;
}
1.000 2.000 -0.667 0.333 2.667
0.000 1.000 -1.667 1.833 1.667
0.000 0.000 1.000 4.375 3.500
0.000 0.000 0.000 1.000 0.800
解は
2.000000
0.200000
0.000000
0.800000
Press any key to continue