データが、ある関数f(x)によって表されとします。ここで、次の量Gを
最小2乗法(1次式)
最小2乗法の利用目的
ある物理学実験から、データが得られたとします。もし、実験から得られたデータが、どのような法則(関数)によって表されるか知らないとしたら、実験で扱った現象を物理学で扱うためにも、どのような法則があるのか調べたいです。そこで用いる方法の1つが最小2乗法です。実験等で得られたデータをある関数で表せると予想し、誤差の評価等に使う方法です。
データが、ある関数f(x)によって表されとします。ここで、次の量Gを
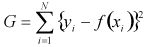 (1.1)
と定義します。
(1.1)
と定義します。 は得られたデータです。目的はこのGを最小にするf(x)を見つけることです。
は得られたデータです。目的はこのGを最小にするf(x)を見つけることです。
データが、ある関数f(x)によって表されとします。ここで、次の量Gを
1次式で近似
f(x)が
 (2.1)
と1次式で表せるとします。この式を(1.1)に代入すると
(2.1)
と1次式で表せるとします。この式を(1.1)に代入すると
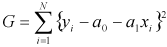 (2.2)
となります。ここでこのGを最小にする係数
(2.2)
となります。ここでこのGを最小にする係数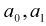 を見つけたい。そのために
を見つけたい。そのために
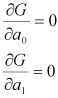 (2.3)
の2つの連立方程式を解きます。(2.3)に(2.2)を代入すると
(2.3)
の2つの連立方程式を解きます。(2.3)に(2.2)を代入すると
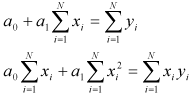 (2.4)
となります。以後表記を簡単にするために
(2.4)
となります。以後表記を簡単にするために
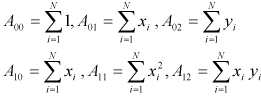 (2.5)
と置いて、(2.4)を
(2.5)
と置いて、(2.4)を
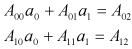 (2.6)
と書き直します。
(2.6)
と書き直します。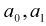 について解くと
について解くと
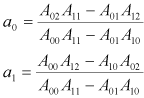 (2.7)
となります。またここで
(2.7)
となります。またここで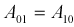 であることを利用し式を整理しています。得られたデータから(2.5)を用いて各Aの値を計算し、(2.7)に代入すれば
であることを利用し式を整理しています。得られたデータから(2.5)を用いて各Aの値を計算し、(2.7)に代入すれば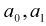 が求まりますので、ゆえに求めたい関数f(x)が決まります。
が求まりますので、ゆえに求めたい関数f(x)が決まります。
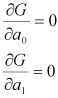 (2.3)
(2.3)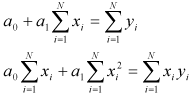 (2.4)
(2.4)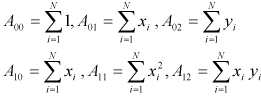 (2.5)
(2.5)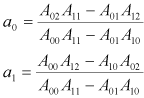 (2.7)
(2.7)プログラムソース
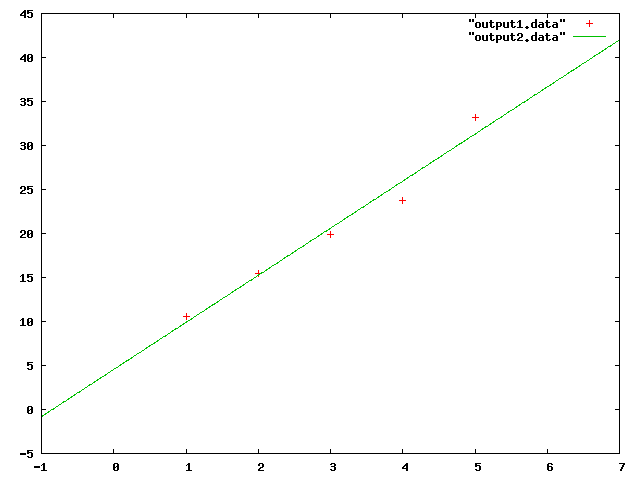
最小2乗法により、1次多項式で近似を行うプログラムです。プログラム中で近似を行ったデータは、適当に決めたものです。ここではデータを直接プログラムソースコード内に記載しています。実際に近似を行うデータは膨大な量になる事が多いですから、その場合はファイルに書き込まれたデータを読み込んで処理するようにプログラムを変更すると良いでしょう。
#include <stdio.h>
#define N 5 //データの個数
void sai1(double x[],double y[])
{
int i;
double a0,a1,p,q;
double A00,A01,A02,A11,A12;
FILE *output1;
FILE *output2;
output1=fopen("output1.data","w");
output2=fopen("output2.data","w");
A00=A01=A02=A11=A12=0.0;
for (i=0;i<N;i++) {
A00+=1.0;
A01+=x[i];
A02+=y[i];
A11+=x[i]*x[i];
A12+=x[i]*y[i];
}
/*1次式の係数の計算*/
a0=(A02*A11-A01*A12)/(A00*A11-A01*A01);
a1=(A00*A12-A01*A02)/(A00*A11-A01*A01);
/*gnuplotでグラフ表示のためにデータをファイルに保存*/
for(i=0;i<N;i++) {
fprintf(output1,"%f %f\n",x[i],y[i]);
}
/*gnuplotでグラフ表示のために
計算で得られた1次式でデータ近辺のグラフデータを保存*/
for(p=x[0]-10.0;p<x[N-1]+10.0;p+=0.01) {
q=a0+a1*p;
fprintf(output2,"%f %f\n",p,q);
}
fclose(output1);
fclose(output2);
}
int main()
{
double x[N]={1.0,2.0,3.0,4.0,5.0},
y[N]={10.6,15.5,19.9,23.8,33.2};
/*横軸(x軸)に値するデータを配列x、
縦軸(y軸)に値するデータを配列yに入れ
関数saiに渡す*/
sai1(x,y);
return 0;
}
数値計算実行結果
2009/04/19 更新