オイラー法

常微分方程式の基本形
において座標点を考え、におけるを求めたいとします。hは微小な値とします。そこでテイラー展開
を用いて式(1)と(2)からhの1次までの項を考えるとすると
という形の式が導けます。この式を利用して数値計算を行っていきますが、テイラー展開の１次までしかとってないので誤差が大きく精度が低いです。

ここでは単振動の問題をオイラー法を使って解いてみます。質量の値とばね定数の値を1とすると運動方程式は
となりますが次のように変形します。
vは速度です。常微分方程式が2つ出てきましたが難しいことはありません。それぞれにオイラー法を適用して解いていきます。

#include <stdio.h>

double f1(double t,double x,double v);
double f2(double t,double x,double v);

int main()
{
        double x,v,t,dt,tmax;
        double k0[2];

        FILE *output;
        output=fopen("output.data","w");

/*初期値*/
        x=1.0;
        v=0.0;
        dt=0.01;
        tmax=100;

        for(t=0.0;t<=tmax;t+=dt) {
                k0[0]=dt*f1(t,x,v);
                k0[1]=dt*f2(t,x,v);
                x=x+k0[0];
                v=v+k0[1];

                fprintf(output,"%f %f %f\n",t,x,v);
        }

        fclose(output);

        return 0;
}

double f1(double t,double x,double v)
{
        return v;
}

double f2(double t,double x,double v)
{
        return (-x);
}

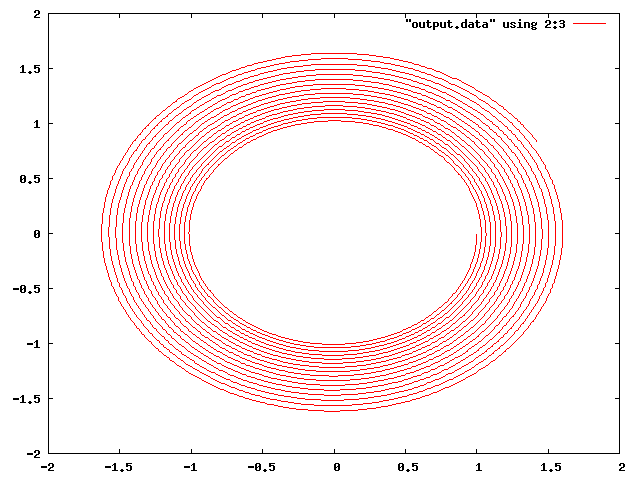
下の画像は数値計算の結果をGNUPLOTで表示したものです。横軸が位置xを表し、縦軸が速度vを表しています。単振動において、外部からの力や摩擦や抵抗がなければ、位置と速度の最大値と最小値は変わらないから、一定の円を描くはずですが、オイラー法で解いた結果はそうなっていません。この原因は誤差によるものです。